What is put call parity in options trading? How is put call parity calculated? Why does it matter?
Put Call Parity - Definition
Put Call Parity is an option pricing concept that requires the extrinsic values of call and put options to be in equilibrium so as to prevent arbitrage. Put Call Parity is also known as the Law Of One Price.
Put Call Parity - Introduction
Put Call Parity is a concept identified by Stoll in 1969, that defines the relationship that must exist in European call and put options. Put options, call options and their underlying stock forms an interrelated securities complex in which the combination of any 2 components yields the same profit/loss profile as the 3rd instrument. Under this kind of complex relationship, no combination of 2 components should yield a position with an asymmetric profit/loss profile as the 3rd instrument so that balance is maintained in the system. This balance is known as the Put Call Parity in option trading. The concept of Put Call Parity is especially important when trading synthetic positions. When there is a mispricing between an instrument and its synthetic position, an options arbitrage opportunity exists.
Put Call Parity requires, mathematically, that option trading positions with similar payoff or risk profiles (i.e Synthetic Positions) must end up with the same profit or loss upon expiration such that no arbitrage opportunities exist. An example of Put Call Parity is in terms of Fiduciary Calls and Protective Puts. Fiduciary Calls and Protective Puts have the same profit/loss profile that you see below. If the underlying stock remains completely stagnant by expiration of both positions, both positions would decline in value equal to the extrinsic value (premium) paid on the options. Neither option trading positions would have any advantage over the other during expiration.
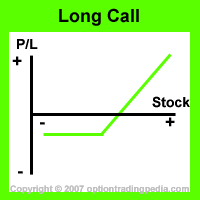
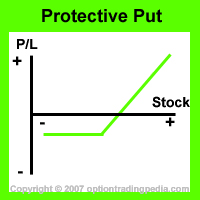
Put Call Parity - An Illustration
To illustrate Put Call Parity at work in option trading, figures are put into both the Fiduciary Calls and Protective Puts positions below:
|
Assume : XYZ shares trading at $50 on 1 Jan. XYZ Feb50Call and Feb50Put are asking at $2.00
Fiduciary Calls : Buy 1 contract of Feb50Call for $200 During expiration of the Feb options, XYZ is still trading at $50 Protective Puts : Lose the whole $200 on the Feb50Puts while the XYZ shares remain stagnant. Net Loss = $200 |
Notice above where Put Call Parity exists, the net loss on both positions are exactly the same so that there are no arbitrage opportunity to be exploited by being long one position and shorting the other simultaneously.
|
Assume : XYZ shares trading at $50 on 1 Jan. XYZ Feb50Call and Feb50Put are asking at $2.00
Fiduciary Calls : Buy 1 contract of Feb50Call for $200 Protective Puts : Buy 100 Shares of XYZ and 1 contract of Feb50Put for a total of $700 During expiration of the Feb options, XYZ is trading at $60. Fiduciary Calls : Profit = [($60 - $50) - $2] x 100 = $800 Protective Puts : XYZ shares gain = ($60 - $50) x 100 = $1000, less loss on put options = $200, net profit = $800 |
Notice above that when Put Call Parity exists, the profit on both positions are also exactly the same. However, the problem is, Put Call Parity rarely exist across the board.
Put Call Parity - The Reality Of Put Call Disparity
As you might have noticed above, Put Call Parity requires that the extrinsic value of call and put options of the same strike price to be the same. However, in reality, the extrinsic value of put and call options are rarely in exact parity in option trading even though market makers have been charged with the responsibility of maintaining Put Call Parity. When the outlook of a stock is bullish, the extrinsic value of call options tend to be higher than put options due to higher implied volatility and when the outlook of a stock is bearish, the extrinsic value of put options tends to be higher than call options.
In the above examples, when the outlook of XYZ stock is bullish, the call options would have a higher extrinsic value than put options, resulting in a higher loss for the Fiduciary Calls than Protective Puts if XYZ shares remain stagnant. In this case, an option arbitrage opportunity would present itself by going long the Protective Puts and going short the Fiduciary Calls. If Fiduciary Calls and Protective Puts are established over a significantly long period of time, the cash reminder of the Fiduciary Calls would also have returned a risk free rate of return, resulting in an arbitrage. However, such option trading arbitrage opportunities are rare even under Put Call Disparity as the presence of bid/ask spreads and commissions tends to neutralise gains from such disparities. In fact, the empirical studies of Kamara and Miller in "Daily and Intradaily Tests of European Put-Call Parity" (JFQA, 30, 1995, No. 4, 519-539) also concluded that even though there are many violations to the Put Call Parity theorem in practise, most of the option trading arbitrage opportunities result in a loss when transaction costs and delays in execution are accounted for.
Deviations from Put Call Parity or Put Call Disparity has also been used in the analysis of future stock prices as stocks with relatively expensive calls have been found empirically to outperform stocks with relatively expensive puts by a measurable significance and margin.
Deviations from Put Call Parity can also lead to profitable arbitrage opportunities using options arbitrage strategies such as a Box Spread if the disparity is significant enough.
Put Call Parity Theorem - Calculating Put Call Parity
The mathematical representation of Put Call Parity in the case of Fiduciary Calls and Protective Puts is:
C + X / (1+RFR)t = S + P
Where : c = Call premium, X / (1+RFR)t = Present value of strike price, S = initial stock price, P = Put premium
Each of the securities in the Put Call Parity Theorem can thus be expressed as:
Stock Price = C - P + X / (1+RFR)t
Put Premium = C - S + X / (1+RFR)t
Call Premium = S + P - X / (1+RFR)t
Present Value Of Strike Price = S + P - C
The above relationships assumes that no dividends are being paid. The Put Call Parity Theorem for dividend paying stocks is:
P = C - S + x/(1+RFR)t + d/(1+RFR)t
C = P + S - x/(1+RFR)t - d/(1+RFR)t
Where d = Dividend To Be Paid
Put Call Parity - Limitations
Put Call Parity applies mainly to European style options as American Style options allows early exercise which can result in profit opportunities that lies beyond the Put Call Parity Theorem.
Put Call Parity - Assumptions
The assumptions under the Put Call Parity Theorem are:
1. Constant Interest Rate
2. Future dividends are known for sure
Important Disclaimer : Options involve risk and are not suitable for all investors. Data and information is provided for informational purposes only, and is not intended for trading purposes. Neither www.optiontradingpedia.com, mastersoequity.com nor any of its data or content providers shall be liable for any errors, omissions, or delays in the content, or for any actions taken in reliance thereon. Data is deemed accurate but is not warranted or guaranteed. optiontradinpedia.com and mastersoequity.com are not a registered broker-dealer and does not endorse or recommend the services of any brokerage company. The brokerage company you select is solely responsible for its services to you. By accessing, viewing, or using this site in any way, you agree to be bound by the above conditions and disclaimers found on this site.
Copyright Warning : All contents and information presented here in www.optiontradingpedia.com are property of www.Optiontradingpedia.com and are not to be copied, redistributed or downloaded in any ways unless in accordance with our quoting policy. We have a comprehensive system to detect plagiarism and will take legal action against any individuals, websites or companies involved. We Take Our Copyright VERY Seriously!
Site Authored by